Alguna vez comenté acerca de combinaciones de números pares e impares. Sin embargo cada combinación de seis números siempre tiene asociada al mismo tiempo una cantidad de números primos y no primos. Esto me llevó a calcular la cantidad de combinaciones posibles considerando tanto números pares como números primos, y el resultado es el siguiente:
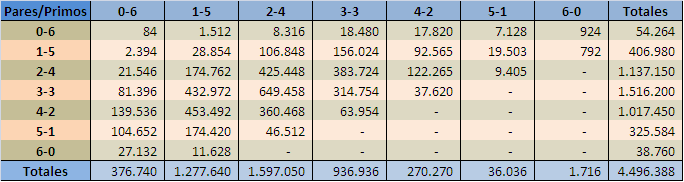
En el cuadro anterior hay casilleros que no contienen cantidades y esto es porque no existen combinaciones posibles que cumplan con la cantidad de números pares y primos correspondientes al casillero; por ejemplo, es imposible encontrar una combinación de seis números del Loto que tenga dos números pares que al mismo tiempo tenga seis números primos, básicamente porque existe sólo un número par que es a la vez primo, el 2.
Si los 1.100 sorteos que se han realizado se hubiesen distribuido uniformemente de acuerdo a las combinaciones posibles, entonces teóricamente tendrían que haber aparecido las siguientes combinaciones:
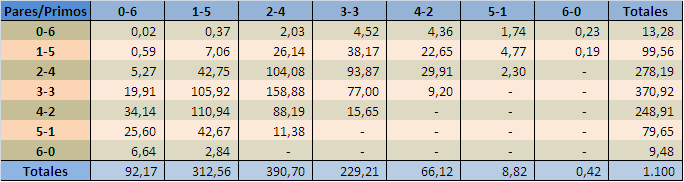
Obviamente los valores en cada casillero se muestran con decimales porque se trata de proporciones y nos sirven como parámetro para comparar con lo que ha sucedido realmente:
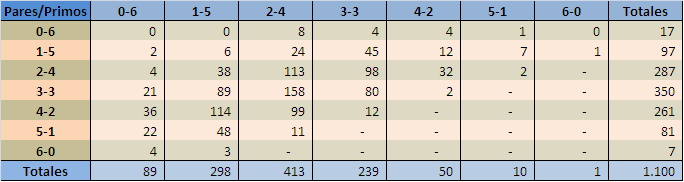
Llama la atención que existen combinaciones que calzan exactamente con lo teórico, por ejemplo la combinación más frecuente (3 pares, 2 primos) que ha salido en 158 ocasiones cuando teóricamente debería haber salido 158,88. En cambio existen otras en que la diferencia es muy grande, por ejemplo 3 pares y 1 primo debería haber aparecido 105,92 veces y ha salido sólo en 89 sorteos, casi 17 veces menos. Pueden sacar sus propias conclusiones, pero si su próxima combinación tiene un número par y cuatro primos, lo entendería perfectamente.



